FP Haskell Haskell98 paper |
"Lazy-evaluation in a functional language is exploited to make the simple dynamic-programming algorithm for the edit-distance problem run quickly on similar strings: being lazy can be fast." [Inf. Proc. Lett., 43(4), pp207-212, Sept' 1992].
a = acgtacgtacgt b = acatacttgtact a = acgtac gtacgt || ||| |||| | b = acatacttgtac t ^ ^^ ^ | || | | || delete | || | insert*2 | change d a b = 4
The algorithm below organises the edit distance "matrix" by diagonals, not by rows or columns. Its time-complexity is O(n×d) where n is the length of the sequences and d is the edit distance between them, i.e. it is fast if the sequences are similar, d<<n. The original program was in Lazy ML; it is given in Haskell 98 here:
module Edit_IPL_V43_N4 (d) where
-- compute the edit distance of sequences a and b.
d a b =
let
-- diagonal from the top-left element
mainDiag = oneDiag a b (head uppers) ( -1 : (head lowers))
-- diagonals above the mainDiag
uppers = eachDiag a b (mainDiag : uppers)
-- diagonals below the mainDiag
lowers = eachDiag b a (mainDiag : lowers) -- !
oneDiag a b diagAbove diagBelow = -- \ \ \
let -- \ \ \
doDiag [] b nw n w = [] -- \ nw n
doDiag a [] nw n w = [] -- \ \
doDiag (a:as) (b:bs) nw n w = -- w me
let me = if a==b then nw -- dynamic programming DPA
else 1+min3 (head w) nw (head n)
in me : (doDiag as bs me (tail n) (tail w))
firstelt = 1+(head diagBelow)
thisdiag =
firstelt:(doDiag a b firstelt diagAbove (tail diagBelow))
in thisdiag
min3 x y z =
-- see L. Allison, Lazy Dynamic-Programming can be Eager
-- Inf. Proc. Letters 43(4) pp207-212, Sept' 1992
if x < y then x else min y z -- makes it O(|a|*D(a,b))
-- min x (min y z) -- makes it O(|a|*|b|)
-- the fast one does not always evaluate all three values.
eachDiag a [] diags = []
eachDiag a (b:bs) (lastDiag:diags) =
let nextDiag = head(tail diags)
in (oneDiag a bs nextDiag lastDiag):(eachDiag a bs diags)
-- which is the diagonal containing the bottom R.H. elt?
lab = (length a) - (length b)
in last( if lab == 0 then mainDiag
else if lab > 0 then lowers !! ( lab-1)
else uppers !! (-lab-1) )
-- module under Gnu `copyleft' GPL General Public Licence.
The code above calculates the value of the edit distance between the sequences a and b only. The "matrix" does contain enough information to recover an alignment of a and b that achieves this value, but this is left as an exercise.
-
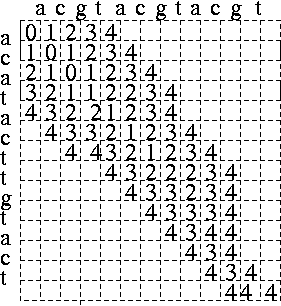
- -- Evaluating O(n×d) entries --
|