Bioinformatics glossary Compression +alignment also see compression(2) Other software: approx.repeats other software |
References
- [PDA98] D.R. Powell, D.L. Dowe, L. Allison and T.I. Dix. Discovering Simple DNA Sequences by Compression. Pacific Symposium on Biocomputing 3 (PSB98), pp.595-606, 1998.
- [AED98] L. Allison, T. Edgoose, & T. I. Dix,
Compression of Strings with Approximate Repeats,
in
Intelligent Systems in Molecular Biology (ISMB'98) , pp.8-16, Montreal,28 June - 1 July 1998 , [pdf]. - [LSE00] L. Allison, L. Stern, T. Edgoose & T. I. Dix.
Sequence Complexity for Biological Sequence Analysis.
Computers and Chemistry 24(1), pp.43-55,
Jan 2000 . - [SAC01] L. Stern, L. Allison, R. L. Coppel & T. I. Dix.
Discovering patterns in Plasmodium falciparum genomic DNA.
Molecular and Biochemical Parasitology,
18(2), pp.175-186,
Dec 2001 . - [CDA07] Minh Duc Cao, T. I. Dix, L. Allison & C. Mears.
A Simple Statistical Algorithm for Biological Sequence Compression.
IEEE Data Compression Conf. (DCC), March 2007 . - [DPA07] T. I. Dix, D. R. Powell, L. Allison, J. Bernal, S. Jaeger, L. Stern.
Comparative Analysis of Long DNA Sequences by Per Element Information Content Using Different Contexts.
BMC Bioinformatics, 8(Suppl.2):S10, 2007. - Also see [more recent].
Demonstration
Below is (i) a repetitive or low-information-content DNA sequence and (ii) a random or high information content sequence.
When analysed the complexity (aka information content, entropy) of a sequence is computed under
- a zero-order Markov model,
- a first-order Markov model, and
- the [AED] model (see refs)
The parameters of a particular model (zero-order MM etc.) are fitted
to the given sequence and the calculations include an estimate
of the cost, in bits, required to state
the parameters of the hypothetical
model (H) to optimum accuracy.
The cost of encoding the data given the model
(D|H) is also given.
The sum, H+(D|H), is the total cost of encoding the sequence
under a particular model.
The model that gives the lowest total cost has the
greatest posterior probability.
Costing H prevents over-fitting:
although a more complex model may fit the data better (D|H),
it has to "pay" for its own great complexity, H.
There is a natural null-hypothesis which is that the sequence
simply consists of random characters and in this case (H)=0
and (D|H)=2 bits/base, for DNA.
Limitations
The demonstration program is a cut-down version. It implements forward approximate repeats only, and is limited to sequences of a few hundred characters because it is run on our web server for demonstration purposes only. The full program implements both forward and reverse complementary approximate repeats and can analyse sequences of hundreds of thousands of characters.
A later algorithm [CDA07 (click)] can run on complete genomes.
Low Information Content Sequence:
- Here is a low-information content sequence:
NB.
It is assumed that the length of the sequence is "common knowledge",
otherwise the length should also be included in the encoding,
using your favourite prior for
lengths.
The formula used to estimate the cost
of the Hypothesis (H) and its parameters
assumes that the sequence is much longer than
the number of parameters
(12 for an first-order MM over DNA).
Random Sequence:
- On the other hand, this is a sequence of 100 bases, generated uniformly and independently at random:
The more complex models find some chance patterns in the sequence and
give a figure of less than
Long Sequences
- The full algorithm (see ref' above)
also implements reverse complementary repeats and,
having certain speed-up techniques,
it can be run on sequences containing
tens or hundreds of thousands of bases (below).
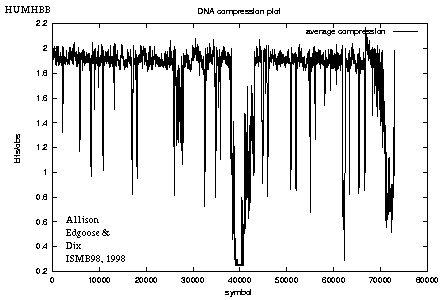
- HUMHBB
Later
A later [algorithm (click)] can be run on complete genomes.
Also See:
- L. Allison.
Information-Theoretic Sequence Alignment (HTML),
TR98/14 School of Comp. Sci. & SWE, Monash University, June 1998,
- on the alignment of non-random
(compressible, repetitive, low-information content) sequences,
[example]. - L. Allison, D. Powell & T. I. Dix.
Compression and Approximate Matching,
Computer Journal , 42(1), pp.1-10, 1999. - D. R. Powell, L. Allison &T. I. Dix.
Modelling alignment for non-random sequences,
Springer Verlag,
AI 2004: Advances in Artificial Intelligence, LNCS/LNAI, vol.3339, pp.203-214, 2004. - Seminars, Sequence Complexity and Alignment (13/2/2001), including some Plasmodium falciparum (malaria) sequences up to about 1 mbp in length,
- Modelling v. Shuffling (11/8/2004),
... on the combination of models(e.g., Probabilistic Finite State Automata, PFSA, Hidden Markov Models, HMM, etc.) of populations with models of pairs of sequences by mutation-machine, or equivalently generation-machine models. - Compression and Analysis of Biological Sequences. Why and How
(2007),
including examples
from the red alga Cyanidioschyzon merolae
and from
p. falciparum . - Information Content Using Different Contexts (2007), with examples of Hepatitis-B (HBV) genomes.
|