Gene Finding With Hidden Markov Models
Seminar by Marina Alexandersson
[email]
of University California at Berkeley
Given at WEHI 11am 5/12/2000
M.A. claimed that HMM based gene finders were the best of those that did not refer to database searches for possible protein matches. Also mentioned that there are "hybrid" schemes that predict and refer to D.B. search
- Hidden Markov Model, underlying Markov process of (hidden) states (used a two-dice example).
- For gene finding, states ~ `intragene', `exon' and `intron'.
- Can attach probabilities to state transistions and to symbols emitted
- Possible questions:
- what is most likely sequence of states | data
- what is probability of data
- what is pr that 3rd item is from state `X', say.
- Discussed order-k Markov chains for k=0, 1, 2, ...
- Noted trade-off of complexity v. fit to data.
Notes taken for the Monash CSSE Bioinformatics group by L.A.
M.A. didn't give any actual % success rates etc.
Did not seem to use any numerical measure of model complexity.
HMM example based on two (the hidden variable) dice.
Intro' to genes, exons, introns [here].
Splice Site Prediction (for intron editing out)
- Use position specific model at exon/intron boundary
- [-8..+17]x4 table, 8 upstream, 17 downstream
Exon Length:
- Could model by `state's - but this gives geometric distribution
- Intron length can be modelled by a geometric dist'n but
- exons lengths not - prob' rises to peak then falls
- Showed length distribution for initial, middle and terminal exons
Positions considered independent - i.e. a "profile" or "block".
You might use mixtures of geometric distributions to flatten out a distribution, but they just don't do peaked distributions. Pity - because geometric d's give linear -log (cost), which has some algorithmic advantages in DPAs.-(
Generalised Hidden Markov Models (GPHMM)
- Presented `Half-Phat' a HMM with 20 states in 4 layers
- intermediate exon layer
- intron layer,
- initial and terminal exon layer,
- integene node.
- intron layer,
- There was replication of exon nodes ~ coding frame.
I'm not sure why this was called "generalised".
Interesting to compare architecture with Glimmer / GlimmerM etc.
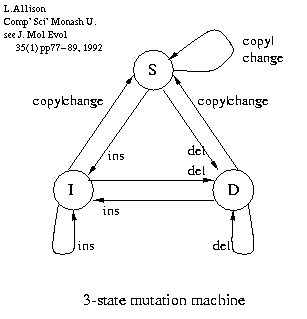
Pair Hidden Markov Models (PHMM) i.e. alignment
<--|
--------------> X---|
| ---<---->--|
| |
begin ---> M -----------------> end
| |
| ---<---->--|
--------------> Y---|
<--|
M - match
X - insert in 1st sequence (or delete)
Y - insert in 2nd sequence.
Algorithms
- Forward algorithm
- Backward algorithm
- Viterbi algorithm
Viterbi on Half-Phat
Showed lattice of states and finding most probably path.
Generalised Pair Hidden Markov Models (GPHMM)
? ~ product of Half_Phat x alignment model, too big to draw.
Double-Phat - two sequence alignment under a gene model.Model Time Space HMM N2.T NT PHMM N2.T.U N.T.U (2 sequences) GHMM D2.N2.T NT GPHMM D4.N2.T.U N.T.U (2 sequences)
where N = # of states, D = max exon length, T=|seq1|, U=|seq2|.
Speed up for GPHMM - get quick alignment, put window around it, work in that area.
Seemed to be related to direct product of
the sequence (gene) machine (model) and
the alignment machine (model).
Interesting to c.f. with:
Allison, Powell & Dix, Compression and approximate matching,
Computer Jrnl. pp1-10, 42(1) 1999.
Also see
[seminar]
3/01.
Could enrich the upstream model, i.e. do something with promoters.
- Limitations and Advantages:
- - can't deal with overlapping genes
- - can't deal with duplications and rearrangements.
- + greatly increased specificity.
- + prediction of weaker signals.
- + several extensions [???]
- - can't deal with duplications and rearrangements.
Acknowledged: Simon Cawley, Lior Pachter, Terry Speed
Nice talk.