[01]
>>
Clustering + a Markov Model
On work by Tim(e) Edgoose
Other debts (alphabetic order):
Rohan Baxter, David Dowe, Chris Wallace.
© 2001 Lloyd Allison,
Computer Science and Software Engineering, Monash University,
Victoria, Australia 3800
This
document is online at
users.monash.edu/~lloyd/Seminars/Mixture-MM/index.shtml
and contains hyper-links to more detailed notes on certain topics
and to some of the references.

<<
[02]
>>
The Problem: Clustering, (unsupervised-) Classification,
Mixture Modelling, Numerical Taxonomy,
in a Time-Series.
Data: A sequence of multi-variate Observations.
- Algorithm based on
[Snob]
which works on independent data.
See
C. S. Wallace & D. M. Boulton.
An Information Measure for Classification.
Computer Journal, 11, pp.185-195, 1968,
and more recently the special issue of the
Computer Journal 42(4) 1999
- Extended:
Observationk can depend on Observationk-1
- i.e. Hidden Markov Model of order 1

<<
[03]
>>
The Model
- (a) The number of classes (N)
- (b) The relative abundance of each class
- (c) For each class
- Distribution parameters for each significant attribute
(e.g. mu, sigma)
- Relative abundance of next class conditional on current class
- (d) For each Observation
- An assigned class (but see twist later)
- Attribute values given this class

<<
[04]
>>

Model Complexity:
- Bayes (1763)
- P(H|D) = P(H) . P(D|H) / P(D)
- Fisher
- Shannon (c1948)
- msgLen(E) = -log2(P(E)) in optimal code,
so . . .
- msgLen(H&D) =
msgLen(H) + msgLen(D|H)
= msgLen(D) + msgLen(H|D)
- msgLen(H) = model complexity
- msgLen(D|H) = data complexity | H

<<
[05]
>>
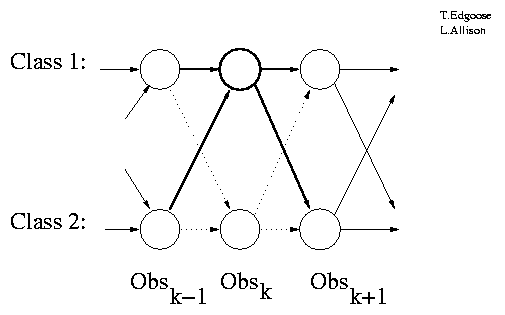
Model Transitions for 2 Classes

<<
[06]
>>
Estimation (1)
- Given an optimal path of transitions through the model, can use
frequencies to estimate transition probabilities etc.
(State to optimum degree of accuracy.)
- New estimates may change optimal path through model.
- Re-estimate, loop, . . . converges.
- (Still have to consider splitting/ merging classes.)
But this gives biased estimates of model parameters!

<<
[07]
>>
Estimation (2) - the twist
- Class memberships of Observations are nuisance parameters
if interested in best class description only.
- Solution: Sum probabilities of all paths through model.
- Legit': Different paths are exclusive sub-hypotheses.
more...

<<
[08]
>>
Forward:
Consider all paths leading to
ok | cj:
- F(o1 in ci) =
P(ci).P(o1|ci)
- F(ok in ci)
= SUMj=1..N F(ok-1 in cj).
P(ci|cj).
P(ok|ci)
- 1 < k <= K
- P(D|H) = SUMi=1..N F(oK in ci)

<<
[09]
>>
Backwards
Consider all paths leading from
ok | cj:
- B(oK in ci) = 1
- B(ok
= SUMj=1..N P(cj|ci).
P(ok+1|cj).
B(ok+1 in cj)
- 1 <= k < K
- Now
- P(D|H, ok in ci)
= F(ok in ci).
B(ok in ci).
- and
- P(D|H) = SUMi=1..N P(D|H, ok in ci)
- for 1 <= k <= K

<<
[10]
>>
. . . this
gives the probability that ok is in cj.
i.e. We can deal with fractional
membership of classes.
Results in unbiased estimates of
class parameters and transition probabilities.

<<
[11]
>>
How Many Classes?
Can split class ci into ci' and ci'',
in ratio w:1-w, e.g. w=0.5.
New transition prob's initialised:
next>
v.
curr'
| . . . | ci' | . . . | ci'' | . . . | cj | . . . |
|---|
.
.
.
| | | | | | | |
|---|
| ci' | | P(ci|ci).w | | P(ci|ci).(1-w) | | P(cj|ci) | |
|---|
.
.
.
| | | | | | | |
|---|
| ci'' | | P(ci|ci).w | | P(ci|ci).(1-w) | | P(cj|ci) | |
|---|
.
.
.
| | | | | | | |
|---|
| cj | | P(ci|cj).w | | P(ci|cj).(1-w) | | | |
|---|
.
.
.
| | | | | | | |
|---|

<<
[12]
>>
Can also merge two classes.
Splitting or merging takes place if there is a nett reduction
in message length.
Good heuristic, fast.
Must converge.
Could get stuck in local optimum, but unlikely.

<<
[13]
>>
Tests, e.g. 2-classes:
varying class auto transition from 0.0 to 1.0
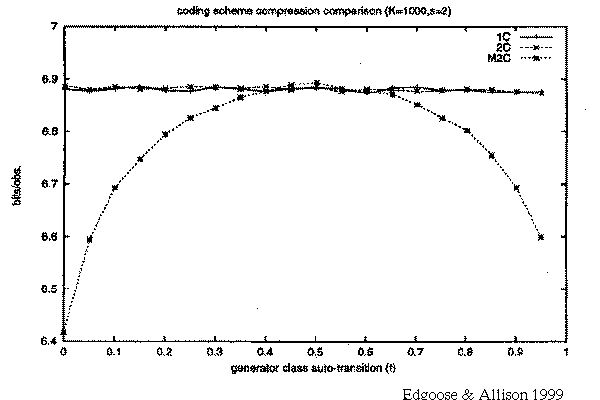

<<
[14]
>>
varying data set size, t=0.8
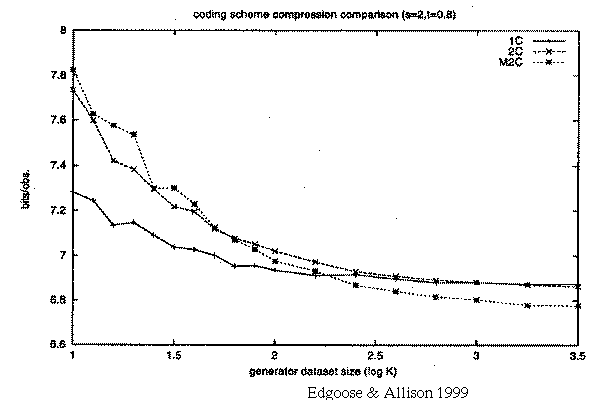
M2C wins if log10(K)>2.3

<<
[15]
>>
e.g. protein dihedral angles:

<<
[16]
Conclusion
- If there is sequential correlation,
the algorithm can better infer class structure from less data
because it models the correlation.
- Time complexity ~ length of sequence × #classes2
- T. Edgoose, L. Allison & D. L. Dowe.
An MML Classification of Protein Sequences that knows about
Angles and Sequences.
Pacific Symposium on Biocomputing, PSB98, pp.585-596, 1998
[paper]
- Tim Edgoose & Lloyd Allison.
Minimum Message Length Hidden Markov Modelling
Data Compression Conf (DCC), pp.169-178, 1998
[paper]
- T. Edgoose & L. Allison.
MML Markov classification of sequential data.
Statistics and Computing 9, pp.269-278, 1999
[paper]