Lectures 7&8
Animals: Form & Function

|
References & Reading Material:
Sims, K. "Evolving Virtual Creatures", proc. SIGGRAPH
1994, ACM Press, pp15-22
Todd, S, Latham, W. "Evolutionary Art & Computers", Academic Press 1992
Reynolds, C.W, "Competition, Co-evolution and the Game of Tag" Artificial
Life IV, Brooks & Maes (eds), MIT Press 1994
van de Panne, M., Fiume, E. "Sensor-Actuator Networks" proc. SIGGRAPH
1993, ACM Press, pp335-342
Koza, J. "Genetic Programming: On the Programming of Computers by Means
of Natural Selection", MIT Press 1992
|
1. Creating Virtual Creatures
A simple model organism can be constructed from three sub-systems:
- A model of organism perception (for input)
- A model of organism computation (for generating behaviour)
- A physical model (for output)
*Note the philosophical standpoint from which such a model stems:
that an organism may be understood as receiving input from the environment,
processing it in some way and then altering/acting on the environment accordingly.
The way an organism behaves is intimately tied to its physical structure.
Eg.
- If you have only one leg you can't run
- If you have no wings you can't fly
- If you have no teeth you can't chew
- If you have eyes you can avoid predators from afar
- If you are tall you can eat leaves from tree-tops etc.
How might it be possible to specify:
- a particular physical model of an organism and
- some high level behaviour...
...and have the computer automatically calculate how the organism might go
about achieving the specified behaviour?
Sample behaviours:
Creature Morphology
- Interesting organism design can lead to interesting methods of locomotion.
- Typically, the more complex a model's structure, the more difficult it is
to successfully animate.
- Artificial evolutionary techniques can be used to design a structure and
its method of locomotion simultaneously and automatically.
- Just as in Dawkin's biomorphs, a genotype
may be created which may develop into a phenotype with (virtual) physical
structure.
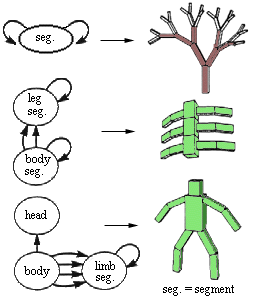
A hierarchy of simple, articulated, rigid primitives may be built from a directed
graph or tree.
The directed graph may be considered to be the genotype of the creature whose
phenotype consists of:
- A physical / visual representation
/ rendered primitives
- The behaviour of the
structure in some environment
The directed graph encodes instructions for growing the creature. Recursion
in the graph provides a means of re-using graph sections to construct organisms
with recursive structure.
|
Genotype: directed graph
|
Phenotype: hierarchy of 3D parts
|
Node data in the graph may describe:
- type of primitive the node represents
- type of joint which connects it to its parent
- number of connections to child nodes
- location, orientation, reflection and scale relative to the parent node
- force which may be applied at the joint
- component's mass and other physical properties
- recursive limit which dictates to what depth the node may recurse
- 'terminal only' flag: causes a connection to be applied at the recursive
limit
- set of neurons (explained shortly)
|
From Sims, "Evolving Virtual Creatures", SIGGRAPH 1994
|
Creature Behaviour
Each creature has a simple brain which:
- accepts input from the sensors
- does some computation
- applies forces and torques at the structure's joints
Internal signals, sensory data and effector data are represented as (positive
or negative) continuous scalar values.
Body-part specific sensors may measure:
- joint angles (continuous)
- contact (binary)
- light source direction (relative vector)
Creature Brain-Power
|
Neurons are implemented as a set of complex functions rather than the
typical threshold/fire model.
Sample neural functions:
sum
product
divide
sum_threshold
greater_than
sign-of
min
max
abs
sin
cos
atan
interpolate
log
integrate
differentiate
smooth
memory
osciallate_wave
oscillate_saw
etc.
Neuronal functions
have parameters which may be constant or may be received from the outputs
of sensors or other neurons.
The genotype, as well as encoding physical topology, encodes the connections
between blocks of neurons.
Here is one of Sims' creatures:
On the right is this virtual creature's brain / controller.
|
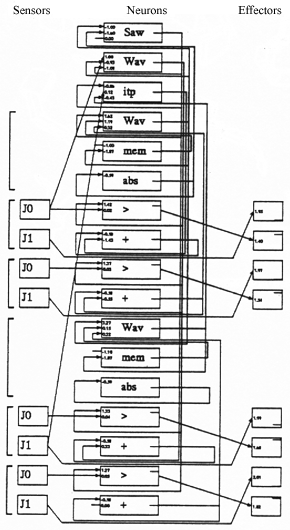
From Sims, "Evolving Virtual Creatures", SIGGRAPH 1994
|
Effectors, Actuators & Creature Control
- The input of an effector
is the output of a single neuron or sensor
- Effectors scale their
input and convert it to a (strength-limited) joint-force
- Blocks of neurons, sensors
and effectors are repeated as determined by a creature's genotype
- Centralized control or
synchronization may arise from a single block of neurons which is not specific
to any body part of the creature. These neurons may communicate with other
parts of the creature's neural network or amongst themselves.
Alternate Methods for Virtual Creature Control
- Look up table for stimulus/response
- Finite State Automata
- Conventional Neural Networks
- Machine Code (or other language)
- Any method for describing algorithms
Obtaining Working Creatures
Constructing complex creatures is not a task suitable for mortals.
The power of genetic algorithmscan be utilized to search the space of possible
organisms for creatures which meet predetermined criteria.
- Begin with a random
population of organisms
- Run a dynamic simulation
of the organisms
- Select the fittest
organisms
(fastest swimmers, highest jumpers etc.)
- Breed the fittest
organisms to produce a new generation
- Return to step
2 until a virtual creature has evolved to meet the requirements
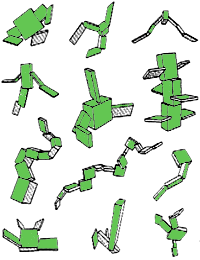
Some creatures evolved by Sims for swimming appear on the right
|
|
Mating Directed Graphs
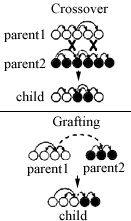
|
In producing a child genotype from two parents:
- Crossover:
copy the genes of one parent into the child's genotype. One or more
crossover points cause a switch to copying the genes from the other
parent.
- Grafting:
Two graphs may be grafted together to form a child.
- The connections of a node are copied with the node.
- Any connections left floating are randomly assigned new terminating
nodes in the child.
- A small amount of mutation may occur in the copying of genes
from a parent to a child. This is implemented as a random change in
a parameter or the re-connection of a link in the graph.
|
2. Introduction to Physically-Based
Modelling
Realistic animation of animal behaviour is (sometimes) achievable through physical
simulation.
Here are four stepping-stones towards physical models of vertebrates.
- Differential Equations
- Particle Dynamics
- Rigid-Body Dynamics
- Articulated-Body Dynamics
Kinematics concerns itself directly with the acceleration, velocity and
position of a body, without reference to the body's mass or the forces required
to move it.
Dynamics concerns itself with the effects of forces applied to a massive
body and the resultant changes in acceleration, velocity and position of that
body.
Differential Equations
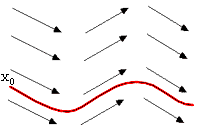
FIG. Path specified through a vector field by an
initial value
|
Of particular interest are initial value problems...
- We are given x(t0) = x0
and wish to follow the change in x forward in time where:
x' = f(x,t)
- The value x0 specifies a path through a vector
field given by the derivative function.
|
Euler's Method
This is a nasty hack (which just about everyone uses anyway)...
x(t + h) = x(t) + h* f(x,t)
The value of x in the future is given by the sum of the current value of x,
and the step size multiplied by the derivative of the function.
(This is just what you are used to doing when you employ the formula: v'=v+at
and s'=s+vt)
Curves and Euler's Method
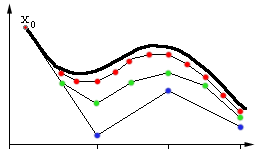 |
When approximating a curve using Euler's method...
- the smaller the step size, the more accurate the approximation of
the curve
- the accumulation of error in Euler's method may be slowed by reducing
the step size, but never eliminated
|
|
Euler's method may be unstable under some circumstances. It may oscillate
about (or even diverge from) the correct value.
The figure shows the inaccuracy of Euler's method: Computing a circular
orbit as a spiral!
|
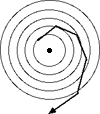 |
Integration using the Runge-Kutta Method
More accurate methods of numerical integration exist. The 4th order Runge-Kutta
scheme is one example:
A measure of the error in such methods can be seen by examining the Taylor's
series expansion:
Consult your nearest Numerical Methods textbook for further details.
Integrating with Adaptive Step Size
- When the function is changing rapidly, small step sizes are needed to approximate
it accurately.
- When the function is changing slowly, large step sizes will save evaluations
and maintain accuracy.
- It is therefore beneficial to have an adaptive step size!
- The step size may be reduced or increased according to an estimate of the
error in approximating the function.
Particle Dynamics
- A particle system is a simple example
of a physically-based model.
- A particle's important characteristics for dynamical simulation (a particle
may be simulated kinematically without all this) are:
- Mass (M)
- Acceleration (A)
- Velocity (V)
- Position (X)
Using Euler's method gives...
- A = Force / M
- V1 = V0 + A * TimeStep
- P1 = P0 + V1 * TimeStep
William, A Two-Mass, One-Spring Worm
A simple dynamical model of worm locomotion may be created using two particles
connected by a spring (or more such systems linked together).
lecture notes | home
All material accessed from www.cs(se).monash.edu.au/~cema
is
© Copyright 1994-2008 Alan Dorin, Jon McCormack & Monash University except where noted.